Dans toute l’étude, on se place dans le cadre du régime permanent, c'est-à-dire que l’on considère les températures (intérieures, extérieures et de surface) comme constante puisque l’énergie perdue à travers la paroi est entièrement complété par l’apport d’énergie du corps de chauffe.

1. Cas d’une paroi simple.

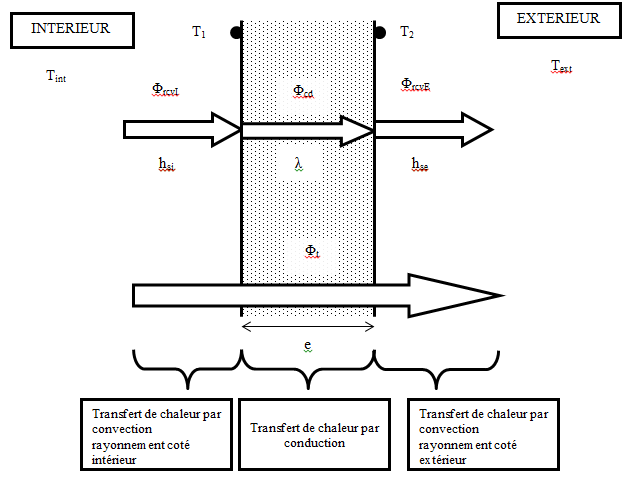
Rappel :

Le principe de conservation de l’énergie implique que :

Φt = Φi = Φcd = Φe

Application au calcul de déperditions

Nous avons une paroi composée de la sorte :

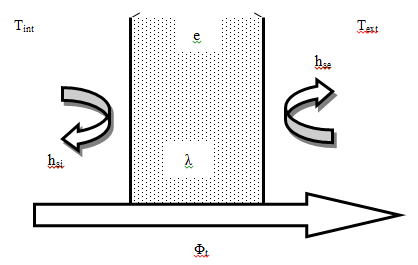
Calcul de la résistante thermique totale équivalente.

Démonstration :

Si on a : Φt = Φi = Φcd = Φe

Alors :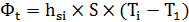        

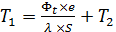
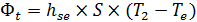                 à          

        à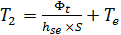        

On en déduit que :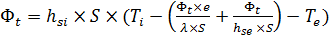                

Donc :

       

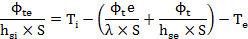
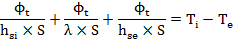
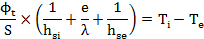
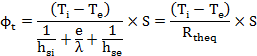
Or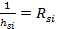        

Et        

Et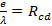        

Donc  Rth = Rcd + Rsi + Rse

On retrouve la loi d’ohm de l’équivalence électrique.

Règles de l’analogie électrique.

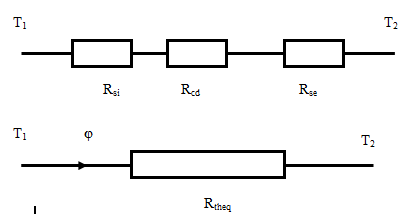
Loi d’ohm :

• En électricité : U = R.I
• En thermique : (Ti – Te) = Rtheq x φ

2. Cas d’une paroi multicouche.

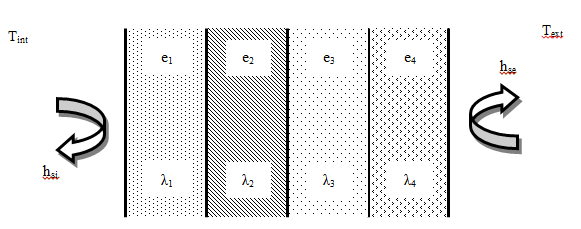
Analogie électrique.

On a :  Rth = Rsi + R1 + R2 + R3 + R4 + Rse

Et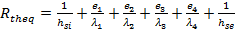  

Remarque :

R est directement donné pour les matériaux hétérogène (ex : parpaing).

Calcul du Ug de la paroi :                                

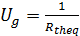
Calcul de la densité de flux surfacique :

( Ti – Te) = Rtheq x φ

donc

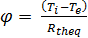
2.1. Calculs des températures intermédiaires.

Pour des problèmes de condensation en surface ou dans les parois, il est intéressant de connaitre les températures intermédiaires entre chaque couche de la paroi.

Méthode :

• Déterminer φ par la méthode précédente.
• Revenir au schéma électrique développé.

• Appliquer la loi d’ohm « thermique » entre 2 points dont celui où l’on cherche la température.

Nota : Il est important de prendre en compte la somme des résistances encadrées par les 2 points.

Created with the Personal Edition of HelpNDoc: Full featured Help generator